Ce cours concerne l'étude de structures algébriques de base (groupes et anneaux) et de leurs propriétés. On met l'accent sur les manipulations effectives.

• Modélisation financière en temps discret
• Modélisation financière en temps continu
• Bases du calcul stochastique

Le programme est organisé autour de tâches relevant des activités langagières définies dans le Cadre européen commun de référence pour les langues (CECR)

• la réception (écouter, lire)
• la production (s'exprimer oralement en continu, écrire)
• l'interaction (prendre part à une discussion)
• la médiation (agir comme un acteur social qui construit, transmet du sens)

Vers la moitié des années ’80 du siècle dernier, lorsque grâce à la correspondance de Curry-Howard le domaine de recherche au carrefour entre l’informatique théorique et la théorie de la démonstration est en plein essor, Jean-Yves Girard introduit et étudie des modèles dénotationnels du système F. Il découvre alors un modèle très simple de F, les espaces cohérents, qui possèdent de remarquables propriétés de dualité, et que les connecteurs de la logique intuitionniste se décomposent au moyen d’opérations plus élémentaires dans ce modèle. Qui plus est, il s’avère que cette décomposition peut être internalisée par le biais de nouveaux connecteurs logiques : c’est ainsi qu’aparaît la Logique Linéaire, comme structure sous-jacente à “la” logique en général, et aux processus calculatoires. La Logique Linéaire est un puissant outil pour analyser et contrôler l’utilisation des ressources en logique et en informatique. Sa nature de structure sous-jacente à la logique a conduit les chercheurs à développer des techniques, des approches et des méthodes qui ont été appliquées dans bien d’autres domaines (théorie de la séquentialité, sémantique de Scott, lambda-calcul, sémantiques de jeux, analyse de la logique classique et de son contenu calculatoire, complexité implicite, vérification, etc.).

Le cours présentera quelques outils fondamentaux de la théorie de la démonstration de la Logique Linéaire. Ils seront introduits à partir des questions qui ont conduit à leur mise au point et on cherchera à mettre en valeur les perspectives écloses par leurs propriétés.

L'apprentissage par renforcement constitue, avec l'apprentissage supervisé et non-supervisé, l'une des trois grandes familles algorithmiques d'apprentissage automatique. Inspirée par la théorie de la décision et la psychologie comportementale, elle a pris une importance de premier plan ces dernières années en fusionnant avec d'autres méthodes d'apprentissage automatique, en particulier celle des réseaux profonds, donnant lieu à des champs d'application encore inexplorés.

Ce cours consiste en une initiation courte à la théorie analytique des nombres. Ce domaine se situe à l'interface avec beaucoup d'autres domaines des mathématiques : formes modulaires, géométrie algébrique, combinatoire ... Il s'agit de donner quelques repères (on démontrera le théorème des nombres premiers) et on évoquera quelques développements très récents sur les fonctions sommatoires de fonctions multiplicatives.

L'objet du cours est une méthode remarquable introduite par Nash et développée par Moser, visant à résoudre des EDO ou des EDP non-linéaires. Cette méthode a été appliquée avec succès à différents problèmes d'analyse et de géométrie : plongement isométrique des variétés, conjugaison des difféomorphismes du cercle, théorème KAM, amortissement Landau...

Le but du cours est d’énoncer les principaux résultats de la « théorie du corps de classes » et d’en donner une démonstration aussi complète que possible dans le temps imparti. Le but de cette théorie est d’obtenir une description des extensions abéliennes d’un corps local ou global en terme de l’arithmétique de ce corps. Le contenu du cours sera utile à tout étudiant intéressé par la théorie des nombres, la géométrie arithmétique ou les formes automorphes.

Le but du cours I est d’introduire les principaux objets qui vont intervenir dans l’énoncé et de démontrer au passage quelques théorèmes classiques de théorie algébrique des nombres. Il a donc un intérêt indépendamment du cours II.

L’objectif du cours est de présenter plusieurs point de vue sur la complexité venant de la logique, de la théorie de la récursion ou de l’analyse. Ces approches ont pour point commun de s’abstraire de la notion de machine (et de ses mesures associées comme le temps et l’espace) au profit d’une vision plus descriptive du calcul. Le cours vise notamment à étudier des formalismes logiques sous l’angle de leur pouvoir d’expression et à présenter de multiples caractérisations des classes de complexité usuelles.

Ces approches de le complexité dîtes descriptives ou implicites ont connu des applications importantes en théorie des bases de données, des langages de programmation ainsi que plus récemment autour de l’analyse des systèmes d’équations différentielles, ou autour de la compréhension de la puissance de modèles alternatifs de calculs basés sur la bioinformatique, ou le calcul analogique.

On visera à présenter dans un premier temps des résultats sur la complexité classique [8, 13], pour aller vers des extensions à des modèles algébriques comme le modèle de Blum Shub et Smale [3, 2], à espace continus comme les modèles de réseaux de neurones/deep learning [17], puis à temps et espace continu comme le modèle de Shannon [16].

Introduire les techniques algorithmiques utilisées en IA pour attaquer des problèmes complexes.

Travail personnel sur une méthode statistique ou une méthode de Mathématiques financières. Exploration de données concrètes. Choix, développement et ajustement d'un modèles. Rédaction d'un rapport.

Ce cours est une introduction aux bases de données à travers l'apprentissage du langage de requêtes SQL et de la modélisation de données dans un modèle relationnel.

Ce cours introduit les outils de base des mathématiques financières et actuarielles, ainsi que les principaux actifs financiers et les produits d’assurance-vie. C’est un prérequis pour les cours de M1 et M2 sur les mathématiques financières, les modèles de taux, ainsi que sur les mathématiques de l’assurance et le risque de longévité.

• Concevoir des composants logiciels réutilisables.
• Comprendre les limites intrinsèques de la POO.
• Compléter l'approche objet à l'aide d'une approche fonctionnelle.
• Utiliser les mécanismes modernes de programmation typée statiquement du langage Scala.
• Savoir apprendre un langage de programmation de façon autonome.
• Analyser des besoins à partir d'une spécification informelle.
• Participer à un processus de développement moderne en utilisant les outils de développement collaboratif et de gestion de projet.
• Utiliser des outils d'intégration continue.

Cours d'anglais de spécialité dispensés par le centre de LANgues pour Spécialistes d'Autres Disciplines (LANSAD).

Rédiger un mémoire sur un sujet choisi avec un enseignant/chercheur du département de mathématiques . Aviser les responsables pédagogiques de l'intitulé du transmettez au chercheur la règle d’évaluation:

• un mémoire -un soutenance de 30mns, de préférence avec un autre chercheur ou enseignant-chercheur dans le jury. Tout doit être fini avant fin juin, pour que la note soit comptabilisée au plus tard dans le jury de seconde session.

Modéliser un phénomène à l'aide d'un système d'équations différentielles ordinaires et/ou à l'aide équations aux dérivées partielles. Caractériser l'existence, l'unicité des solutions. Caractériser les propriétés de ces éventuelles solutions. Approcher numériquement ces solutions par des algorithmes stables et efficaces. Coder ces algorithmes. Utiliser les bibliothèques de résolution disponibles en Scilab/Python.

Ce cours est une continuation naturelle du cours "Calculabilité et incomplétude" du premier semestre. Les travaux de Godel, Church, Turing et d'autres, sur la définition formelle d'ensemble calculable, ont posés les bases sur lesquelles allait s'échafauder l'étude des degrés d'insolubilité : un important corpus de connaissances permettant de classer et comprendre l'univers des objets incalculables. Nous mèneront durant ce cours une étude détaillée de cet univers.

La calculabilité a aussi obtenu des succès majeurs en fournissant un cadre formel pour l'étude de certaines questions épistémologiques. Nous en verrons un exemple avec l'étude de l'aléatoire algorithmique. Nous verrons comment utiliser la calculabilité pour étudier avec une approche mathématique la question informelle de ce qu'est une suite de bits ``aléatoire''.

La deuxième partie du cours traite de la complexité de Kolmogorov. On donnera les définitions et les propriétés élémentaires. Nous verrons comment on utilise la complexité algorithmique dans les preuves de complexité. Nous étudierons les objets aléatoires finis et infinis.

Ce projet est conçu en partenariat avec RCI Renault Crédit International et offre aux étudiants l’opportunité d’effectuer une mission Data Science dans un cadre professionnel.

Le brief de la mission est proposé par RCI – par exemple un problème de score d’octroi sur des données extraites du data warehouse du donneur d’ordre RCI. Le cadrage est effectué par RCI et Karine Tribouley. Les étudiants effectuent la mission

• Production de solutions : méthodes et codes
• Mise en avant des performances des solutions
• Rédaction des livrables : rapports et codes

Pour le langage/logiciel à utiliser, R ou Python sont très fortement recommandés même si les étudiants sont libres de choisir d'autres langages ou logiciels parmi le C, le C#, Matlab, SAS, etc.

L’objectif de ce cours est de présenter les risques principaux auxquels sont confrontés les acteurs financiers, au premier rang desquels les banques mais aussi les assurances, les catégoriser, les quantifier et enfin les gérer. Le cours s’attachera à faire le lien avec les techniques de modélisation des risques et leur application dans le cadre de la réglementation bancaire. Un point d’attention sera notamment dédié aux risques climatiques.

Ce cours a vocation tout d’abord à fournir aux étudiants les éléments théoriques fondamentaux de la gestion d’actifs, de la modélisation des actifs eux-mêmes, de la construction d’un portefeuille théorique, pour aboutir à l’analyse structurée d’un portefeuille existant, tant du point de vue de l’analyse financière que de l’analyse statistique.

Il s’agit d’un cours de programmation en langage Python, dans la perspective de l’utiliser pour le calcul scientifique et l’analyse des données, avec également une introduction aux librairies de machine learning pytorch et tensorflow.

• Familiarisation avec les principales méthodes du traitement automatique des langues (TAL)
• Appliquer des notions d'apprentissage à la modélisation du langage. Cas de l'apprentissage structuré (séquences et arbres)
• Présentation / utilisation des principales librairies incluant des modules de TAL prêts à l'emploi (Spacy, NLTK)
• Présentation / utilisation de librairies génériques d'apprentissage profond pour le TAL (pytorch)

Consolidation des connaissances en algorithmique, connaissance des rudiments de la complexité et des approches algorithmiques classiques.

Le cours est en partie mutualisé avec le master Math-Info.

• les étudiants du M1 mathématiques suivent les deux parties du cours (sur 12 semaines)
• les étudiants du M1 mathématiques-informatique suivent la seconde partie du cours (sur les 8 dernières semaines). Les étudiants de cette filière peuvent néanmoins suivre la première partie s'ils le désirent.

Ce cours est le second volet d'un parcours explorant les liens profond existant entre les algèbres d’opérateurs, la théorie géométrique et la théorie mesurée des groupes discrets dénombrables. Les algèbres d’opérateurs, introduites par Murray et von Neumann entre 1940 et 1950 dans l’optique de formaliser les concepts de la mécanique quantique, ont connu des progrès spectaculaires, en lien avec la théorie ergodique et la théorie des groupes, ces 15 dernières années. Ce parcours présentera quelques uns de ces résultats très récents ainsi que les techniques modernes qui permettent de les obtenir.

Dans ce second cours, différentes propriétés d’approximations pour les groupes et algèbres de von Neumann, dont l’utilisation permet d’obtenir des résultats surprenant de rigidité, seront présentées et étudiées en détails.

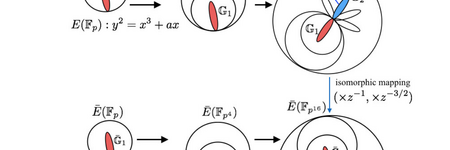
Le projet est l'occasion de travailler un algorithme ou un protocole cryptographique de manière approfondie, en visant compréhension théorique et mise en œuvre algorithmique.

Les étudiants rédigent un mémoire (~15 pages) et réalisent une implantation informatique dont les performances sont démontrées lors de l'oral de soutenance. Le projet est réalisé en binôme.

• Maîtriser la notion de transaction.
• Maîtriser l'organisation physique de la base de données et la gestion des transactions.
• Maitriser les triggers.
• Normalisation de bases de données

Les formes du général

Le thème principal du cours est l’interaction entre la logique et les jeux. De nombreux exemples d’une telle interaction existent, notamment la clôture stratégique et la détermination en théorie des ensembles, les jeux de Ehrenfeucht-Fraïssé en théorie des modèles, le jeux des cailloux en complexité descriptive et d’arguments de décision en théorie d’automates. Pour citer Jouko Väänänen, il y a trois sortes de jeux en logique, les trois en connexion étroite. Il nomme cette connexion « l’équilibre stratégique en logique ». Le cours sera librement inspiré par cette connexion et basé sur le livre « Models and games » par Väänänen, avec d’explorations supplémentaires en théorie descriptive des ensembles, les grands cardinaux et la décidabilité.

L'objectif de ce cours est d’abord de présenter les notions logiques de décidabilité et d'indécidabilité. On définit ensuite la notion de réduction entre problèmes. On présente enfin la notion de complexité qui prend en compte les ressources (temps de calcul, espace mémoire) nécessaires à la résolution d’un problème sur machine.

Maîtrise des techniques d'optimisation utilisées en Machine Learning

Maîtriser la planification l'exécution et l'optimisation de requêtes. Savoir-faire attendu d'un architecte de données

On propose une introduction à la géométrie sous-riemannienne, notamment autour des questions de l'existence, caractérisation et régularité des géodésiques sous-riemanniennes. On introduira notamment le formalisme hamiltonien, qui est le langage naturel pour traiter ce genre de problèmes.

Prérequis:

Géométrie différentielle et Riemannienne (le cours de J. Marché à P6 ou [2] chapitres1-6, ou encore [1]) Équations aux dérivées partielles principalement elliptiques (Le cours de Yves Achdou & Xavier Blanc à P7 ou [3] chapitres 5-6)

Le but du cours est d’énoncer les principaux résultats de la « théorie du corps de classes » et d’en donner une démonstration aussi complète que possible dans le temps imparti. Le but de cette théorie est d’obtenir une description des extensions abéliennes d’un corps local ou global en terme de l’arithmétique de ce corps. Le contenu du cours sera utile à tout étudiant intéressé par la théorie des nombres, la géométrie arithmétique ou les formes automorphes.

• Langages, structures, théories du premier ordre
• Ultraproduits, compacité.
• Extensions élémentaires, Théorèmes de Lowenheim-Skolem, chaînes élémentaires.
• Théorèmes de préservation.
• Va et vients.
• Élimination des quantificateurs, modèle-complétude.
• Espace des types.
• (Si le temps le permet) Typer réalisés et types omis, modèles atomiques.

Il s’agit d’une introduction au langage C# et par là même aux concepts de programmation orientée objet et de programmation fonctionnelle. On montre sur des exemples (et des exercices) comment ces notions facilitent la création de programmes pour répondre à des problèmes algorithmiques et mathématiques. Le cours comprend 10 séances de 4h (1/4 de cours et 3/4 de travaux pratiques). L’évaluation est basée sur une séance de TP notée, un examen écrit et un projet (en 2020 le projet porte sur l’algorithme MCTS pour les jeux).

Ce cours d'algèbre se concentre sur trois aspects :

• étude approfondie de la divisibilité dans les anneaux (anneaux factoriels, notamment) ;
• modules de type fini sur un anneau principal, application à l'algèbre linéaire ($K[T]$-modules) et aux groupes abéliens de type fini ($\mathbb{Z}$-modules) ;
• représentations linéaires des groupes finis.

À ce niveau, il est intéressant de :

• donner des exemples sophistiqués — par exemple, pour les algèbres
  • corps non commutatifs (quaternions de Hamilton),
  • algèbre d'un groupe pour le produit de convolution (sous diverses formes, algébrique $K^{(G)}$, mesures de probabilité, algèbres des fonctions intégrables sur $\mathbb{R}$, éventuellement périodiques...)
• mettre en évidence les propriétés universelles de certaines constructions ;
• éventuellement, mettre en place le vocabulaire catégorique ;
• dans une direction opposée, expliquer aussi des méthodes algorithmiques pour effectuer certaines opérations algébriques (déterminer un générateur d'un groupe cyclique dont on connaît le cardinal, par exemple, ou bien une base d'un $\mathbb{Z}$-module, par opérations sur les lignes...)

L'objectif du cours est de rendre les étudiants de M2 ISIFAR opérationnels, dans la perspective des stages notamment, pour tout ce qui concerne les méthodes de pricing et couverture en finance, aussi bien d'un point de vue modèles que produits et implémentation. On aborde également les aspects calibration de modèles. Des scripts en python sont mis à la disposition des étudiants pour qu'ils les exécutent, interprètent, complètent, en lien avec le cours. Une mini-librairie de pricing en C++ est distribuée en open source (calcul avec les nombres complexes pour pricing par Fourier, outils d'algèbre linéaire, de simulation pseudo et quasi aléatoire...) et à coder par les étudiants. A nouveau, certaines fonctions ne sont que typées et le corps des fonctions est à coder par les étudiants.

Le calcul des probabilités est un outil de modélisation construit sur des fondements issus de l'analyse: la théorie de la mesure et de l'intégration. Ce cours est illustré par une étude détaillée du comportement des collections de variables indépendantes. L'analyse permet de définir et d'étudier la convergence des suites de variables aléatoires. Les notions et techniques utiles aux statisticiennes et aux physiciens sont définies et étudiées ici: convergence en probabilités, loi des grands nombres, convergence en loi, théorème central limite. Le cours propose une construction de l'espérance conditionnelle, outil indispensable pour la théorie des martingales, le calcul stochastique, l'inférence bayésienne, et donc pour les mathématiques financières, les statistiques et bien d'autres spécialités. Enfin le cours abordera les inégalités de concentration, outil de la théorie de l'apprentissage.

• Pricing d'options Européennes dans un modèle discret à plusieurs périodes; cas du modèle de Cox-Ross-Rubinstein
• Arrêt optimal et application au pricing d'options Américaines
• Introduction au mouvement brownien et au calcul stochastique d'Itô.
• Pricing d'options dans le modèle de Black et Scholes

• Calculabilité : fonctions récursives et fonctions calculables par machine ; caractérisation logique des fonctions calculables ; théorème smn et théorèmes de point fixe ; notions de réduction et problèmes indécidables.
• Introduction à la complexité : classes en temps et espace, théorèmes de hiérarchie, réductions, complétude, circuits booléens, introduction à la complexité algébrique.
• Arithmétique formelle : axiomes de Peano et sous-systèmes faibles ; arithmétisation de la logique ; théorèmes d’indécidabilité ; les théorèmes d’incomplétude de Gödel.

• Théorème de complétude du calcul des séquents égalitaire LK par les témoins de Henkin.
• Calcul des séquents : Élimination des coupures et théorème du séquent médian dans LK. Théorème de Herbrand. Sous-calcul LJ : la logique intuitionniste et son interprétation BHK. Propriétés de la sous-formule et du témoin existentiel dans LJ.
• Déduction naturelle : Systèmes NK et NJ. Élimination des coupures de NJ. Propriétés de la sous-formule et du témoin existentiel dans NJ, puis dans HA (arithmétique intuitionniste).
• Lambda-calcul : Propriétés de confluence et de standardisation. Représentation des fonctions récursives. Système T. Correspondance de Curry-Howard. Réalisabilité, normalisation forte et correction des programmes.

La théorie de l'homotopie, ou l'étude des espaces topologiques à déformation près, a fait surgir une branche de l'algèbre appelée algèbre homotopique, où sont développés les outils pour la description de structures où les lois telles que l'associativité ne sont plus vérifiées exactement comme en algèbre classique, mais à homotopie près, ces homotopies étant elles-mêmes sujettes à des cohérences, et ainsi de suite.

La théorie de l'homotopie a aussi une dimension logique, avec l'interprétation de la notion de type comme espace, de preuve d'égalité comme chemin dans un espace et de preuve d'égalité de preuves d'égalité comme une homotopie entre chemins. Ces liens ont donné naissance à la théorie homotopique des types. La notion de fibration, qui joue un rôle essentiel en théorie de l'homotopie, est intimement liée à la notion de substitution en théorie des types dépendants.

Le cours, qui fera suite au cours de théorie des catégories du premier semestre, mais peut être suivi par des étudiants ayant déjà acquis ces bases par ailleurs, introduira les notions importantes sous-jacentes au domaine: les catégories enrichies, les catégories de modèles, et différentes façons de définir les catégories supérieures, notamment via les ensembles simpliciaux. Seront abordés aussi des sujets connexes comme les opérades et les ∞-opérades, eux aussi issus de la topologie. Le cours s'appuiera en partie sur plusieurs ouvrages parus dans les années récentes (Categorical homotopy theory d' Emily Riehl, The homotopy theory of (∞, 1)-categories de Julia Bergner, From categories to homotopy theory de Birgit Richter, Higher categories and homotopical algebra de Denis-Charles Cisinski, Simplicial methods for higher categories de Simona Paoli, qui offrent autant de lectures d'approfondissement pour les étudiantes et étudiants intéressés), avec une attention portée aux liens avec la théorie homotopique des types.

L'objectif du cours de "probabilités et extrêmes" est de donner les bases mathématiques fondamentales pour l'étude ultérieure de modèles stochastiques, de modèles du risque et des questions de modélisation aléatoire ou statistique. Les outils probabilistes fondamentaux sont présentés dans ce cours (vecteurs gaussiens, loi conditionnelle, théorie des martingales, théorie des valeurs extrêmes, chaines de Markov). Ils sont un prérequis fondamental à l'étude des processus en temps continu comme les processus de Poisson et le calcul stochastique.

Ce cours a pour but de comprendre les protocoles de la cryptologie à clé publique et les mathématiques sur lesquelles ils reposent.

Ce cours étudiera sous différents aspects la notion de second-ordre en logique et étudiera les logiques à points-fixes. On abordera notamment différentes applications informatiques de ces formalismes logiques à l'étude des langages formels sur les mots et les arbres et à l'étude des langages de programmation.

L’objectif de ce cours est de donner une introduction à la théorie des représentations des algèbres semi-simples, en particulier des algèbres de groupes finis, et d’étudier plus précisément celles des groupes symétriques en interaction avec le groupe linéaire.

Présentation de méthodes d'apprentissage supervisé et non-supervisé : classification par les centres mobiles, modèles de mélange gaussien, analyse discriminante linéaire et quadratique, régression logistique, classifieurs des plus proches voisins et à noyau, arbres de décision, méthodes bagging, boosting et forêts aléatoires, machines à vecteurs de support, régression Ridge ou Lasso, réseaux de neurones. Des exercices pratiques sur machine complèteront le cours.

Ce cours a pour but de comprendre comment améliorer la fiabilité des transmissions de données grâce à des principes d'algèbre.

Ce cours a pour but de comprendre les protocoles de la cryptologie symétrique et d'assimiler les notions de complexité dans une pratique réelle de la cryptologie.

En termes modèle-théoriques, une expansion M du corps ordonné des réels est o-minimale si tout sous-ensemble M-définissable de R a un nombre fini de composantes connexes. Ceci peut être également formulé en des termes purement géométriques, en tant que propriété d'une collection d'ensembles réels stable par les opération booléennes ensemblistes, produits cartésiens et projections linéaires. Les ensembles définissables dans une structure o-minimale partagent de nombreuses bonnes propriétés topologiques avec les ensembles algébriques et analytiques réels (théorie de la dimension, finitude uniforme, stratification), d'où l'intérêt pour la géométrie o-minimale en lien avec la géométrie Diophantienne et arithmétique, les systèmes dynamiques non-oscillants et l'analyse asymptotique. Je donnerai une vue d'ensemble des résultats principaux sur les structures o-minimales et ensuite j'illustrerai les principales méthodes pour démontrer qu'une collection de fonctions réelles engendre une structure o-minimale. Il n'y a essentiellement pas de prérequis pour ce cours, outre que les notions de base d'algèbre et d'analyse acquises en licence : les notions de théorie de modèles nécessaires sont minimales et je fournirai de la bibliographie sur le sujet si besoin.

Ce cours a pour objectif de présenter différentes techniques d'apprentissage supervisé (en classification et en régression) et non supervisé. L'apprentissage statistique désigne un ensemble de méthodes et d'algorithmes permettant d'extraire des informations pertinentes d'un ensemble de données et d'apprendre des comportements à partir d'exemples.

Le 8 août 1900, lors du second Congrès International des mathématiciens, à Paris, David Hilbert énonça une liste de 23 problèmes mathématiques qui, selon lui, devaient servir de guide pour les recherches à venir dans le nouveau siècle. Le premier problème de cette liste, l’hypothèse du continu de Cantor, a été résolu, en deux temps : par Gödel (1938) qui construisit un modèle interne de l'hypothèse généralisée du continu, et par Paul Cohen (1963), qui a inventé une construction de modèle pour la négation de l’hypothèse de Cantor. Ce cours couvrira principalement les deux constructions de modèles de la théorie des ensembles introduites par Gödel et Cohen.

• Calcul des propositions : tables de vérité, tautologies, formes normales, compacité.
• Calcul des prédicats : langages du premier ordre, termes, formules, modèles ; satisfaction d’une formule dans un modèle ; sous-structures ; isomorphismes ; équivalence élémentaire.
• Théorie des ensembles : axiomes de Zermelo-Frænkel ; cardinaux ; théorèmes de Cantor et de Cantor- Bernstein ; ensembles finis, ensembles dénombrables.
• Introduction à la programmation : Mise à niveau en programmation fonctionnelle Ocaml ; Lien avec le lambda-calcul, récursivité, typage ML ; structures de données usuelles (booléens, entiers, listes, options, arbres, ...).

Le but de ce cours est de présenter des avancements récents sur la géométrie d’Arakelov birationnelle. La géométrie d’Arakelov est une théorie de géométrie arithmétique, où plusieurs domaines mathématiques, comme géométrie algébrique, théorie des nombres, géométrie analytique interviennent naturellement. Elle consiste à «compactifier» les variétés sur un corps de nombres par des objets analytiques, en s’appuyant sur la comparaison avec la géométrie algébrique relativement à une courbe projective régulière.

Le cours commence par une introduction sur la géométrie des nombres classique et sa version moderne dans le langage de fibré vectoriel hermitien. Ensuite on introduit une géométrie de courbe adélique dont le corps «de nombres» sous-jacent est de type fini sur Q.

La géométrie algébrique est l'étude des « objets » géométriques définis par des équations polynomiales. Un premier chapitre du cours reprend donc l'étude de l'anneau des polynômes en plusieurs variables et expose en particulier la correspondance entre algèbre (idéaux radicaux) et géométrie (parties fermées pour la topologie de Zariski) lorsque le corps de base est algébriquement clos. Le cours se poursuit avec l'introduction de l'espace projectif. À ce stade de l'élaboration du programme, les deux derniers chapitres sont des propositions. La première exposerait la théorie des courbes planes et notamment le théorème de Bézout sur le nombre de points d'intersection de deux courbes. La seconde introduirait des rudiments de géométrie algébrique réelle, où un phénomène nouveau apparaît.

L'objectif de ce cours est d'exposer, d'un point de vue théorique mais sans recours excessif aux outils mathématiques, les méthodes indispensables à l'usage des statistiques inférentielles en milieu professionnel. Le cours magistral (2 h) introduit la modélisation statistique; il est accompagné de travaux dirigés (2h) et de travaux pratiques (2h) en langage R dont la connaissance parfaite est un pré-requis pour s'orienter vers la data science.

Savoir manipuler des outils d'analyse dans le cadre de la dimension infinie. Mise en oeuvre dans le cadre des espaces de fonctions

Entrainement et usage des réseaux de neurones profonds

Projet sur un sujet de statistique ou d'analyse numérique à choisir dans une liste proposée par les responsables.

Ce cours est une introduction au langage Statistical Analysis System dit SAS. Ce langage est très largement adopté dans les entreprises utilisant des données (banques, assurances, services, industries, ..) et une bonne maîtrise de ce langage est souvent un pré-requis dans les offres d’emplois ou de stages ciblant les étudiants des filières statistiques.

• Les axiomes de ZF
• Ordinaux, Cardinaux, récurrence transfinie
• Arithmétique ordinaux et cardinaux
• Axiom du Choix et équivalents, filtres et ultrafiltres
• Cofinalité, cardinaux réguliers/singuliers, théorème de König
• Ensembles stationnaires, clubs, Lemma de Fodor
• Absoluité et théorèmes de reflexion
• L'universe constructible

L'objectif de ce cours est de comprendre les principaux défis posés par les données en grande dimension en statistique.

On propose une introduction à la géométrie sous-riemannienne, notamment autour des questions de l'existence, caractérisation et régularité des géodésiques sous-riemanniennes. On introduira notamment le formalisme hamiltonien, qui est le langage naturel pour traiter ce genre de problèmes.

Le cours s'articule autour de trois résultats fondateurs de Claude Shannon. Ce sont trois théorèmes mathématiques portant sur des problèmes de numérisation optimale et de transmission de l'information.

Le premier théorème s'intéresse à la compression des données : si on veut numériser un document, il est intuitivement clair qu'on va gagner en espace de stockage en codant de façon plus courte les caractères les plus fréquents et de façon plus longue les moins fréquents. Cette fréquence des caractères nous fera introduire le langage des probabilités et d'entropie de Shannon.

Le deuxième théorème s'intéresse à la transmission (ou stockage) sans pertes des données. On démontre qu'en introduisant un peu de redondance dans un document numérisé, on peut le retrouver malgré la perte aléatoire d'une partie de l'information. C'est encore ici le langage des probabilités qui est utilisé. En plus de l'entropie, apparaît ici la notion de capacité d'un canal de transmission.

Le troisième est le théorème d'échantillonnage. Une information peut être une fonction d'une variable réelle. Le théorème d'échantillonnage nous explique comment, en prenant la valeur de cette fonction en un nombre fini de points, on peut reconstruire l'information. On tient compte pour cela des fréquences de notre fonction. L'analyse faite ici est basée sur la théorie des séries de Fourier.

Ce cours introduit les outils de base des mathématiques financières et actuarielles, ainsi que les produits financiers et les contrats d'assurance-vie. C'est un pré-requis pour les cours de M2 portant sur les mathématiques de la finance ou de l'assurance.

Connaître les principales techniques d'algorithmique et savoir évaluer leur complexité

L'objectif du cours est de maîtriser les modèles et méthodes stochastiques utilisés dans les salles de marché et d'acquérir les premières notions de la gestion des risques financiers. Les aspects mathématiques et financiers seront présentés en parallèle ; les nouveaux concepts mathématiques seront immédiatement illustrés par leurs applications à la finance. Pour le côté mathématique on abordera notamment le mouvement brownien et l'intégration stochastique ; la formule d'Itô, le changement de probabilité et les équations différentielles stochastiques. Pour le côté finance, on étudiera le modèle de Black et Scholes et ses extensions ; la technique de changement de numéraire ; la diffusion implicite de Dupire ; la valorisation d'options exotiques par Monte Carlo. Une place importante sera dédiée à la simulation, afin que les connaissances acquises soient directement opérationnelles. L'accent sera également mis sur la compréhension des limites de la modélisation, pour bien identifier les risques associés.

L'algorithmique des données massives, des flots, de la cryptologie utilisent la randomisation (les tirages aléatoires), et l'approximation pour traîter des problèmes qui sans cela seraient difficiles. Ce cours est approche systématique de ces méthodes et des méthodes de traitement distribuées.

Le cours présente les concepts fondamentaux de la théorie des catégories, illustrés de nombreux exemples. L’objectif essentiel est préparer l’accès aux applications actuelles des catégories en logique, en informatique théorique et en théorie de l’homotopie.

Théorie des types de base:

• Système de types purs
• Théorie des types de Martin-Löf
• Calcul des constructions inductives
• La correspondance preuve/programme
• Discernabilité et indiscernabilité des preuves − Types inductifs et coinductifs
• Extensionalité en théorie des types

Théorie des types homotopique :

• La correspondance type/espace, égalité/chemin
• Concepts homotopiques en théorie des types (espaces contractibles, h-niveaux, univalence, systèmes de factorisation faibles, fibrations, cofibrations)
• Type inductifs supérieurs (sphères, quotients, troncations,...)
• Axiome du choix et logique classique en théorie des types homotopique

Modèles :

• Catégories de famille
• Théorie des types cubique − Traductions internes
• ω-groupoïdes
• Complexes de Kan

Ce cours a pour but de maîtriser les concepts de base du langage C. L'objectif à l'issue du semestre est d'être capable de programmer en utilisant les principales librairies du langage

Les données sont des résultats d'expériences ou d'enquêtes mesurés, observés, sur un certain nombre d’individus. Il s'agit soit de nombres (variable quantitative), soit de codes (variable qualitative)

L’analyse des données est un outil perfectionné de statistique descriptive, qui consiste à étudier un jeu de données individus x variables en recherchant notamment s'il existe des relations entre individus et entre variables

On peut distinguer 3 groupes de méthodes : la statistique descriptive classique qui permet l’étude d'une ou deux variables observées sur un ensemble d'individus, des analyses portant sur des nuages de points de plus grande dimension, ainsi que la classification automatique consistant à regrouper des individus en catégories homogènes relativement à tel ou tel critère

Comme les tableaux de données peuvent être très grands en pratique, ce qui nécessite des calculs sur ordinateurs, le module comprend des séances de Travaux Pratiques avec le logiciel R

Ce cours est le troisième volet d'un parcours explorant les liens profond existant entre les algèbres d’opérateurs, la théorie géométrique et la théorie mesurée des groupes discrets dénombrables. Les algèbres d’opérateurs, introduites par Murray et von Neumann entre 1940 et 1950 dans l’optique de formaliser les concepts de la mécanique quantique, ont connu des progrès spectaculaires, en lien avec la théorie ergodique et la théorie des groupes, ces 15 dernières années. Ce parcours présentera quelques uns de ces résultats très récents ainsi que les techniques modernes qui permettent de les obtenir.

Ce troisième cours portera sur les sous algèbres abéliennes maximales d’une algèbre de von Neumann finie. On étudiera en détail le lien entre ces dernières et les actions préservant une mesure de probabilité de groupes dénombrables. Plusieurs résultats profonds, tels que l’unicité de la Cartan dans le facteur hyperfini II1 (Connes-Feldman-Weiss, 1981) et la trivialité du groupe fondamental de L(SL2(Z)nZ2) (Popa, 2001), seront démontrés.

L'objectif de ce cours est l'étude des modèles stochastiques de taux d'intérêt et des méthodes du pricing pour les dérivés de taux. Dans un premier temps les notions de base et les produits dérivés présents sur les marchés de taux seront introduits. La modélisation stochastique de taux d'intérêt sera étudié dans les cadres suivantes : modèles de taux court, modèle Heath-JarrowMorton et modèle de marché Libor (modèle BGM). Dans chacun de ces modèles les conditions de l'absence d'arbitrage seront trouvées et des méthodes du pricing risque-neutre des options seront présentées. Les modèles de taux plus récents dits multicourbe seront abordés à la fin du semestre.

Ce cours entend fournir aux étudiants les principes de base des mathématiques de l'assurance. Dans ce cours, on aborde la théorie économique à la base des choix d'assurance, les méthodes de calcul des primes, les mesures de risque et la détermination de la marge de solvabilité ainsi que du capital économique.

Renforcer la maîtrise des concepts liés au paradigme de programmation objets en montrant comment ils peuvent être implantés différemment. Apprendre le langage C++.

Intervention 2022 : Google

Intervention 2022 : Barclays

Le but de ce cours est d'introduire à la théorie des représentations dite "supérieure", où les espaces vectoriels sont remplacés par des catégories et les actions par des foncteurs. Cette approche permet de démontrer, entre autres : des propriétés de positivité et des identités combinatoires (en "décatégorifiant"), des équivalences entre catégories abéliennes ou triangulées,l'existence de bases "canoniques" pour certaines représentations.

Ce cours s'insère dans la filière "Algèbre, groupes et représentations" mais certaines constructions topologiques (faisceaux constructibles et faisceaux pervers) seront aussi évoquées.

Mettre en œuvre les méthodes d’exploration classique: régression, réduction de dimension, classification. Usage des outils de visualisation et de manipulation de données (R/Python)

Le but de ce cours est de présenter des avancements récents sur la géométrie d’Arakelov birationnelle. La géométrie d’Arakelov est une théorie de géométrie arithmétique, où plusieurs domaines mathématiques, comme géométrie algébrique, théorie des nombres, géométrie analytique interviennent naturellement. Elle consiste à «compactifier» les variétés sur un corps de nombres par des objets analytiques, en s’appuyant sur la comparaison avec la géométrie algébrique relativement à une courbe projective régulière.

La dernière partie du cours porte sur un travail récent en collaboration avec Moriwaki sur l’étude des schémas projectifs au-dessus d’une courbe adélique générale et leurs invariants arithmétiques.

Ce cours a pour objectif de présenter des sujets liés à la modélisation stochastique du business de l'assurance qui aujourd’hui sont la base des cadres d’analyse de la valorisation et du risque des compagnies d’assurances.

La géométrie algébrique est l'étude des ensembles définis des équations polynomiales à plusieurs variables à coefficients dans un corps, appelés variétés affines. On considère aussi les sous-ensembles des espaces projectifs définis par des équations polynomiales homogènes, de façon à obtenir des objets « compacts », les variétés projectives. Dès qu'on a défini les concepts de dimension et de lissité, on peut entamer un travail de classification (à isomorphisme près) des variétés projectives lisses connexes de dimension donnée, sur un corps fixé qui sera pour nous le corps des complexes. En dimension 1, on appelle ces variétés des courbes et un élément essentiel de leur classification est leur genre, un entier positif. Dès la dimension 2, la classification demande plus de travail mais est maintenant bien comprise depuis des décennies.

Les surfaces K3 seront le fil conducteur du cours mais j'en profiterai pour introduire divers outils classiques utilisés dans l'étude des surfaces algébriques.

Une moitié des heures de ces modules consistera en des cours, l’autre en des TP sur machine. Ces cours se concluront par un projet à réaliser en Coq. Le contenu de ces cours est un prérequis pour le cours de théorie des types homotopiques.

Ce cours est le premier volet d'un parcours explorant les liens profond existant entre les algèbres d’opérateurs, la théorie géométrique et la théorie mesurée des groupes discrets dénombrables. Les algèbres d’opérateurs, introduites par Murray et von Neumann entre 1940 et 1950 dans l’optique de formaliser les concepts de la mécanique quantique, ont connu des progrès spectaculaires, en lien avec la théorie ergodique et la théorie des groupes, ces 15 dernières années. Ce parcours présentera quelques uns de ces résultats très récents ainsi que les techniques modernes qui permettent de les obtenir.

Le premier cours de ce parcours est une introduction aux algèbres d’opérateurs : C*-algèbres et algèbres de von Neumann.

Ce cours vise à présenter les fondements logiques et informatiques des blockchains (protocoles de communications, théorie des jeux), ainsi que des exemples de protocoles mis en oeuvre en particulier dans les crypto-monnaies et les smart-contracts. Nous consacrerons une partie substantielle du cours à l’examen de la "finance décentralisée” c’est-à-dire l’ensemble des contrats existants sur chaine qui reporoduisent et pour certains étendent les pratiques financières.

Ce cours sera une continuation naturelle du cours de théorie des modèles du premier semestre. On cherchera à comprendre et classifier les modèles d'une théorie du 1er ordre donnée à travers les types que l'on peut réaliser ou omettre.

Usage des méthodes randomisées en traitement des données massives et en traitement des flots de données (streaming). Familiarisation avec Spark. Articulation estimation/optimisation

La théorie de la démonstration a connu au moins deux évolutions majeures au cours du siècle dernier suite aux théorèmes d'incomplétude de Gödel. La première a eu lieu dans les années 30, immédiatement après les résultats d'incomplétude, avec l'introduction et l'étude de la déduction naturelle et du calcul des séquents par Gentzen et du lambda-calcul par Church. Church montrait alors l'indécidabilité du calcul des prédicats via le lambda-calcul tout en introduisant un modèle de calcul universel tandis que Gentzen déduisait la consistance de divers systèmes logiques comme corollaire de l'élimination des coupures en calcul des séquents.

La seconde étape a eu lieu dans les années 60 avec la mise en évidence progressive, par le biais de la correspondance de Curry-Howard, des liens profonds entre preuves et programmes, depuis la correspondance entre lambda-calcul simplement typé et déduction naturelle propositionnelle minimale jusqu'aux diverses extensions de cette correspondance au second ordre, à la logique classique et jusqu'à l'émergence de la notion de linéarité en théorie de la démonstration. La logique linéaire a profondément renouvelé les liens entre la sémantique formelle des langages de programmation d'un côté et la théorie de la démonstration de l'autre. L'algèbre linéaire s'impose comme troisième pôle de cette correspondance, en mettant au centre la notion de ressource du calcul.

Le cours fondamental a traité de la première étape. Ce cours sera consacré à quelques développements plus récents.

Ce cours étudiera sous différents aspects la notion de second-ordre en logique et étudiera les logiques à points-fixes. On abordera notamment différentes applications informatiques de ces formalismes logiques à l'étude des langages formels sur les mots et les arbres et à l'étude des langages de programmation.

Le codage consiste à protéger une information de la dégradation physique, en lui ajoutant une redondance structurée. L'enjeu de la cryptographie est de maîtriser l'accès à des données ou des services, et les protéger de modifications ou copies malveillantes.

Ce cours est à la fois une introduction détaillée à ces domaines, et un cours d'algorithmique algébrique Dans ce cours, on décrit les bases théoriques de ces domaines et les principaux systèmes utilisés. On apprend aussi les techniques d'algorithmique algébrique employées pour les mettre en œuvre, ou pour attaquer les cryptosystèmes.

Le module de projet est l'occasion d'approfondir des thèmes qui ne sont qu'évoqués dans ce cours.

La statistique mathématique permet d'ajuster un modèle probabiliste aux observations effectuées sur un phénomène. Ce modèle ajusté peut être utilisé pour expliquer (physique, ...), déterminer des causes (santé, ...), évaluer des risques (assurance, environnement, ...), ou prédire (notations, décision, ...). Ce cours introduit la statistique mathématique dans cette perspective. A l'issue de ce cours, vous saurez

• Construire un modèle statistique.
• Construire et valider un estimateur.
• Réaliser un test binaire.
• Choisir et valider un modèle.

Le cours s'appuie sur un environnement de calcul statistique (R ou Python)

• Connaitre les technologies modernes pour le traitement de données massives.
• Maitriser l’utilisation de librairies pour le traitement de données distribuées.
• Etre capable d’utiliser ces outils dans des cas concrets, en utilisant une solution cloud.